Abstract: This paper addresses the problem of variance estimation for a general U-statistic. U-statistics form a class of unbiased estimators for those parameters of interest that can be written as E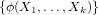, where ϕ is a symmetric kernel function with k arguments. Although estimating the variance of a U-statistic is clearly of interest, asymptotic results for a general U-statistic are not necessarily reliable when the kernel size k is not negligible compared with the sample size n. Such situations arise in cross-validation and other nonparametric risk estimation problems. On the other hand, the exact closed form variance is complicated in form, especially when both k and n are large. We have devised an unbiased variance estimator for a general U-statistic. It can be written as a quadratic form of the kernel function ϕ and is applicable as long as k ≤ n∕2. In addition, it can be represented in a familiar analysis of variance form as a contrast of between-class and within-class variation. As a further step to make the proposed variance estimator more practical, we developed a partition resampling scheme that can be used to realize the U-statistic and its variance estimator simultaneously with high computational efficiency. A data example in the context of model selection is provided. To study our estimator, we construct a U-statistic cross-validation tool, akin to the bic criterion for model selection. With our variance estimator we can test which model has the smallest risk.

Key words and phrases: Best unbiased estimator, cross-validation, likelihood risk, model selection, partition resampling, U-statistic, variance.