



Statistica Sinica 10(2000), 297-315
LOCAL COMPARISON OF RAO AND WALD STATISTICS
IN THE BAHADUR SENSE
Yoshihide Kakizawa
Hokkaido University
Abstract:
Global optimality of likelihood ratio test statistics is well-known
in the Bahadur sense. In this paper the behaviors of Rao and Wald
statistics (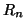 and
and 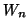 )
for testing
)
for testing
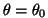 are studied.
It turns out that at alternative
are studied.
It turns out that at alternative
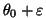 ,
the Bahadur slopes of these two statistics for the one-sided case are
identical up to order
,
the Bahadur slopes of these two statistics for the one-sided case are
identical up to order 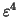 ,
while for the two-sided case,
they are identical only up to order
,
while for the two-sided case,
they are identical only up to order 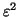 ,
in general i.i.d. models and Gaussian stationary processes.
We obtain the second- (first-) order Bahadur efficiency of
,
in general i.i.d. models and Gaussian stationary processes.
We obtain the second- (first-) order Bahadur efficiency of
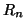 and
and 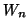 for the one- (two-) sided case.
The third-order Bahadur efficiency depends on the statistical curvature.
Two concrete examples are given. One is a curved exponential family,
and the other is a Gaussian AR(1) process.
The latter provides an example that the
for the one- (two-) sided case.
The third-order Bahadur efficiency depends on the statistical curvature.
Two concrete examples are given. One is a curved exponential family,
and the other is a Gaussian AR(1) process.
The latter provides an example that the 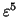 -term of the Bahadur
slope of
-term of the Bahadur
slope of 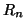 for the one-sided case is different from that of
for the one-sided case is different from that of 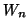 .
.
Key words and phrases:
Bahadur slope, curved exponential family,
Gaussian stationary process, large deviation theorem, Rao's statistic,
spectral density, Wald's statistic.








and
) for testing
are studied. It turns out that at alternative
, the Bahadur slopes of these two statistics for the one-sided case are identical up to order
, while for the two-sided case, they are identical only up to order
, in general i.i.d. models and Gaussian stationary processes. We obtain the second- (first-) order Bahadur efficiency of
and
for the one- (two-) sided case. The third-order Bahadur efficiency depends on the statistical curvature. Two concrete examples are given. One is a curved exponential family, and the other is a Gaussian AR(1) process. The latter provides an example that the
-term of the Bahadur slope of
for the one-sided case is different from that of
.



