Statistica Sinica
3(1993), 481-500
ORDER DETERMINATION FOR AUTOREGRESSIVE
PROCESSES USING RESAMPLING METHODS
Changhua Chen, Richard A. Davis, Peter J. Brockwell and Zhi Dong
Bai*
Colorado State University and Temple University*
Abstract:
Let
X1, ..., Xn
be observations from an AR(p)
model with unknown order
p.
A resampling procedure is proposed for estimating the order p.
The
classical criteria, such as AIC and BIC, estimate the order p
as the
minimizer of the function
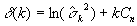
where n
is the sample size, k
is the order of the fitted model
, 
is an estimate of the white noise variance, and Cn
is a
sequence of specified constants (for AIC, Cn=2/n
,
for Hannan and Quinn's
modification of BIC,
Cn=2(lnln n)/n
.
Often, the traditional order
selectors overfit or underfit the model for a given realization. To overcome
this defect, a resampling scheme is proposed to estimate a suitable penalty
factor Cn.
Conditional on the data, this procedure produces a consistent
estimate of p.
Simulation results support the effectiveness of the procedure
when compared with some of the traditional order selection criteria for both
Gaussian and a range of non-Gaussian processes. A discussion of the merits of
Yule-Walker estimation relative to Burg and maximum likelihood estimation for
order determination is also given.
Key words and phrases:
Autoregressive processes, order determination, AIC, Yule-Walker estimation,
resampling.