Abstract: Given a sample of size from a population of individuals belonging to
different species with unknown proportions, a problem of practical interest consists
in making inference on the probability
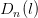 that the
-th draw coincides with a species with frequency
that the
-th draw coincides with a species with frequency
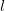 in the sample, for any
in the sample, for any
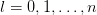 . This paper contributes to the methodology of Bayesian nonparametric inference for
. This paper contributes to the methodology of Bayesian nonparametric inference for
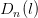 Specifically, under the general framework of Gibbs-type priors we show how to
derive credible intervals for a Bayesian nonparametric estimation of
Specifically, under the general framework of Gibbs-type priors we show how to
derive credible intervals for a Bayesian nonparametric estimation of
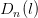 , and
we investigate the large
, and
we investigate the large
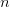 asymptotic behaviour of such an estimator. Of particular
interest are special cases of our results obtained under the specification of
the two parameter Poisson–Dirichlet prior and the normalized generalized Gamma
prior. With respect for these prior specifications, the proposed results are illustrated
through a simulation study and a benchmark Expressed Sequence Tags dataset. To
the best our knowledge, this provides the first comparative study between the twoparameter
Poisson–Dirichlet prior and the normalized generalized Gamma prior in
the context of Bayesian nonparemetric inference for
asymptotic behaviour of such an estimator. Of particular
interest are special cases of our results obtained under the specification of
the two parameter Poisson–Dirichlet prior and the normalized generalized Gamma
prior. With respect for these prior specifications, the proposed results are illustrated
through a simulation study and a benchmark Expressed Sequence Tags dataset. To
the best our knowledge, this provides the first comparative study between the twoparameter
Poisson–Dirichlet prior and the normalized generalized Gamma prior in
the context of Bayesian nonparemetric inference for
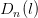 .
.
Key words and phrases: Asymptotics, Bayesian nonparametrics, credible intervals, discovery probability, Gibbs-type priors, Good–Turing estimator, normalized generalized Gamma prior, smoothing technique, two-parameter Poisson–Dirichlet.



