Abstract: The appearance of massive data has become increasingly common
in contemporary scientific research. When the sample size n is huge, classical
learning methods become computationally costly in regression analysis.
Recently, the orthogonal greedy algorithm (OGA) has been revitalized as an
efficient alternative in the context of kernel-based statistical learning. In a
learning problem, accurate and fast prediction is often of interest. This makes
an appropriate termination crucial for OGA. In this paper, we propose a
new termination rule for OGA via investigating its predictive performance.
The proposed rule is conceptually simple and convenient for implementation,
which suggests an O(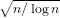 ) number of essential updates in an OGA
process. It therefore provides an appealing route to conduct efficient learning
for massive data. With a sample dependent kernel dictionary, we show that
the proposed method is strongly consistent with an O(
) number of essential updates in an OGA
process. It therefore provides an appealing route to conduct efficient learning
for massive data. With a sample dependent kernel dictionary, we show that
the proposed method is strongly consistent with an O(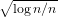 ) convergence
rate to the oracle prediction. The promising performance of the method is
supported by simulation and data examples.
) convergence
rate to the oracle prediction. The promising performance of the method is
supported by simulation and data examples.
Key words and phrases: Forward regression, greedy algorithms, kernel methods, massive data, nonparametric regression, sparse modeling.



