Abstract: Variable selection is considered in the setting of supervised binary
classification with functional data {X(t), t ∈ [0,1]}. By “variable selection”
we mean any dimension-reduction method that leads to the replacement
of the whole trajectory {X(t), t ∈ [0,1]}, with a low-dimensional vector
(X(t1),…,X(td)) still keeping a similar classification error. Our proposal for
variable selection is based on the idea of selecting the local maxima (t1,…,td)
of the function 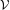 X2(t) =
X2(t) = 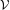 2(X(t),Y ), where
2(X(t),Y ), where 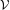 denotes the “distance
covariance” association measure for random variables due to Székely, Rizzo,
and Bakirov (2007). This method provides a simple natural way to deal with
the relevance vs. redundancy trade-off which typically appears in variable
selection. A result of consistent estimation for the maxima of
denotes the “distance
covariance” association measure for random variables due to Székely, Rizzo,
and Bakirov (2007). This method provides a simple natural way to deal with
the relevance vs. redundancy trade-off which typically appears in variable
selection. A result of consistent estimation for the maxima of 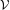 X2 is shown.
We also show different models for the underlying process X(t) under which
the relevant information is concentrated on the maxima of
X2 is shown.
We also show different models for the underlying process X(t) under which
the relevant information is concentrated on the maxima of 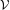 X2. An extensive
empirical study is presented, including about 400 simulated models and
data examples aimed at comparing our variable selection method with other
standard proposals for dimension reduction.
X2. An extensive
empirical study is presented, including about 400 simulated models and
data examples aimed at comparing our variable selection method with other
standard proposals for dimension reduction.
Key words and phrases: Distance correlation, functional data analysis, supervised classification, variable selection.



