



Statistica Sinica 11(2001), 479-498
ON BAHADUR EFFICIENCY AND MAXIMUM LIKELIHOOD
ESTIMATION IN GENERAL PARAMETER SPACES
Xiaotong Shen
The Ohio State University
Abstract:
The paper studies large deviations of maximum likelihood and related
estimates in the case of i.i.d. observations with distribution determined
by a parameter 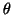 taking values in a general
metric space. The main theorems provide sufficient conditions under which
an approximate sieve maximum likelihood estimate is an asymptotically locally
optimal estimate of
taking values in a general
metric space. The main theorems provide sufficient conditions under which
an approximate sieve maximum likelihood estimate is an asymptotically locally
optimal estimate of 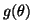 in the sense of Bahadur, for virtually all
functions
in the sense of Bahadur, for virtually all
functions 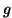 of interest. These conditions are illustrated by application
to several parametric, nonparametric, and semiparametric examples.
of interest. These conditions are illustrated by application
to several parametric, nonparametric, and semiparametric examples.
Key words and phrases:
Asymptotic optimality,
Bahadur bound, large deviations, maximum likelihood estimation,
nonparametric and semiparametric models, the method of sieves.








taking values in a general metric space. The main theorems provide sufficient conditions under which an approximate sieve maximum likelihood estimate is an asymptotically locally optimal estimate of
in the sense of Bahadur, for virtually all functions
of interest. These conditions are illustrated by application to several parametric, nonparametric, and semiparametric examples.



