Statistica Sinica 10(2000), 1199-1215

ESTIMATION OF KENDALL'S TAU UNDER CENSORING

Weijing Wang and Martin T. Wells

National Chiao-Tung University and Cornell University

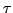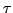Abstract: We study nonparametric estimation of Kendall's tau, , for bivariate censored data. Previous estimators of , proposed by Brown, Hollander and Korwar (1974), Weier and Basu (1980) and Oakes (1982), fail to be consistent when marginals are dependent. Here we express 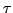as an integral functional of the bivariate survival function and construct a natural estimator via the von Mises functional approach. This does not necessarily yield a consistent estimator since tail region information on the survival curve may not be identifiable due to right censoring. To assess the magnitude of the inconsistency we propose some estimable bounds on . 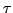It is shown that estimates of the bounds shrink to provide consistency if the largest observations on both marginal coordinates are uncensored and satisfy certain regularity conditions. The bounds depend on the sample size, on censoring rates and, in particular, on the estimated probability of the unknown tail region. We also discuss using the bootstrap method for variance estimation and bias correction. Two illustrative data examples are analyzed, as well as some simulation results.

Key words and phrases: Bivariate censored data, bivariate survival function estimation, bootstrap, rank correlation, V-statistic, von Mises functional.