Statistica Sinica 10(2000), 73-91
BETA KERNEL SMOOTHERS FOR REGRESSION CURVES
Song Xi Chen
La Trobe University
Abstract:
This paper proposes beta kernel smoothers for estimating
curves with compact support by employing a
beta family of densities as kernels.
These beta kernel smoothers are free of boundary bias,
achieve the optimal convergence
rate of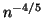 
for and always allocate
non-negative weights. In the
context of regression, a comparison is made between
one of the beta smoothers and the local linear smoother.
Its is comparable with that of the .
Situations where the beta kernel
smoother has a smaller are given. Extensions to
probability density
estimation are discussed.
Key
words and phrases:
Beta kernels, boundary bias, local linear regression,
mean integrated square error, nonparametric regression.