Abstract: Computing posterior modes (e.g., maximum likelihood estimates) for models involving latent variables or missing data often involves complicated optimization procedures. By splitting this task into two simpler parts, however, EM-type algorithms often offer a simple solution. Although this approach has proven useful, in some settings even these simpler tasks are challenging. In particular, computations involving latent variables are typically difficult to simplify. Thus, in models such as hierarchical models with complicated latent variable structures, computationally intensive methods may be required for the expectation step of EM. This paper describes how nesting two or more EM algorithms can take advantage of closed form conditional expectations and lead to algorithms which converge faster, are straightforward to implement, and enjoy stable convergence properties. Methodology to monitor convergence of nested EM algorithms is developed using importance and bridge sampling. The strategy is applied to hierarchical probit and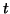regression models to derive algorithms which incorporate aspects of Monte-Carlo EM, PX-EM, and nesting in order to combine computational efficiency with easy implementation.
Key words and phrases: Bridge sampling, efficient data augmentation, Gibbs sampler, GLMM, hierarchical models, importance sampling, MCEM algorithm, MCMC, probit models, t-models, working parameters.