


Abstract: Let pi(w),i = 1,2, be two densities with common support where each density is known up to a normalizing constant: pi(w) = qi(w)/ci. We have draws from each density (e.g., via Markov chain Monte Carlo), and we want to use these draws to simulate the ratio of the normalizing constants, c1/c2. Such a computational problem is often encountered in likelihood and Bayesian inference, and arises in fields such as physics and genetics. Many methods proposed in statistical and other literature (e.g., computational physics) for dealing with this problem are based on various special cases of the following simple identity:
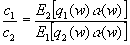
Here Ei denotes the expectation with respect to pi (i=1,2), and α is an arbitrary function such that the denominator is non-zero. A main purpose of this paper is to provide a theoretical study of the usefulness of this identity, with focus on (asymptotically) optimal and practical choices of α . Using a simple but informative example, we demonstrate that with sensible (not necessarily optimal) choices of α , we can reduce the simulation error by orders of magnitude when compared to the conventional importance sampling method, which corresponds to α =1/q2. We also introduce several generalizations of this identity for handling more complicated settings (e.g., estimating several ratios simultaneously) and pose several open problems that appear to have practical as well as theoretical value. Furthermore, we discuss related theoretical and empirical work.
Key words and phrases: Bridge sampling, Bayes factor, Hellinger distance, importance sampling, iterative simulation, likelihood ratio, free-energy difference, posterior odds, Markov chain Monte Carlo.