Abstract: In semiparametric and nonparametric statistical inference, the asymptotic normality of estimators has been widely established when they are
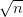 -consistent. In many applications, nonparametric estimators are not able to achieve this rate. We have a result on the asymptotic normality of nonparametric
- estimators that can be used if the rate of convergence of an estimator is
-consistent. In many applications, nonparametric estimators are not able to achieve this rate. We have a result on the asymptotic normality of nonparametric
- estimators that can be used if the rate of convergence of an estimator is
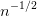 or slower. We apply this to study the asymptotic distribution of sieve estimators of functionals of a mean function from a counting process, and develop nonparametric tests for the problem of treatment comparison with panel count data. The test statistics are constructed with spline likelihood estimators instead of nonparametric likelihood estimators. The new tests have a more general and simpler structure and are easy to implement. Simulation studies show that the proposed tests perform well even for small sample sizes. We find that a new test is always powerful for all the situations considered and is thus robust. For illustration, a data analysis example is provided.
or slower. We apply this to study the asymptotic distribution of sieve estimators of functionals of a mean function from a counting process, and develop nonparametric tests for the problem of treatment comparison with panel count data. The test statistics are constructed with spline likelihood estimators instead of nonparametric likelihood estimators. The new tests have a more general and simpler structure and are easy to implement. Simulation studies show that the proposed tests perform well even for small sample sizes. We find that a new test is always powerful for all the situations considered and is thus robust. For illustration, a data analysis example is provided.
Key words and phrases: Asymptotic normality, - estimators, nonparametric maximum likelihood, nonparametric maximum pseudo-likelihood, nonparametric tests, spline.



